
В отличие от этого, стандартное отклонение - это квадратный корень из числового значения, полученного при расчете дисперсии. Многие люди противопоставляют эти два математических понятия. Итак, в этой статье делается попытка пролить свет на важное различие между дисперсией и стандартным отклонением.
Сравнительная таблица
| Основа для сравнения | отклонение | Стандартное отклонение |
|---|---|---|
| Имея в виду | Дисперсия - это числовое значение, которое описывает изменчивость наблюдений от ее среднего арифметического. | Стандартное отклонение - это мера дисперсии наблюдений в наборе данных. |
| Что это? | Это среднее квадратов отклонений. | Это среднеквадратичное отклонение. |
| Помечены как | Сигма-квадрат (σ ^ 2) | Сигма (σ) |
| Выражено в | Квадратные единицы | Те же единицы, что и значения в наборе данных. |
| Указывает | Как далеко люди в группе разбросаны. | Сколько наблюдений за набором данных отличается от его среднего значения. |
Определение дисперсии
В статистике дисперсия определяется как мера изменчивости, которая показывает, как далеко распределены члены группы. Он определяет среднюю степень, в которой каждое наблюдение отличается от среднего. Когда дисперсия набора данных мала, это показывает близость данных к среднему значению, тогда как большее значение дисперсии показывает, что наблюдения очень рассеяны вокруг среднего арифметического и друг от друга.
Для неклассифицированных данных :
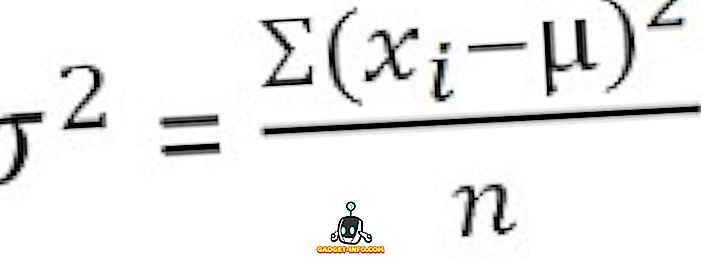
Для сгруппированного распределения частот :
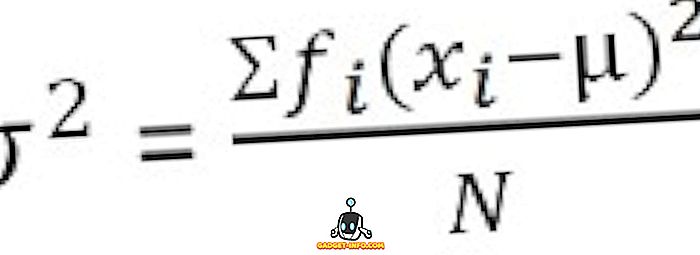
Определение стандартного отклонения
Стандартное отклонение - это мера, которая количественно определяет степень разброса наблюдений в наборе данных. Низкое стандартное отклонение является показателем близости оценок к среднему арифметическому, а высокое стандартное отклонение представляет; баллы разбросаны по более высокому диапазону значений.
Для неклассифицированных данных :

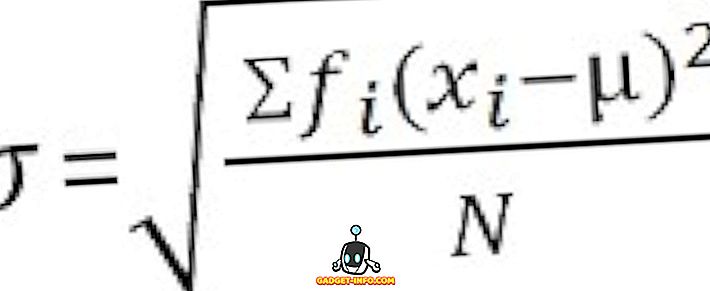
Ключевые различия между дисперсией и стандартным отклонением
Разницу между стандартным отклонением и дисперсией можно четко разграничить по следующим причинам:
- Дисперсия - это числовое значение, которое описывает изменчивость наблюдений от ее среднего арифметического. Стандартное отклонение - это мера дисперсии наблюдений в наборе данных.
- Дисперсия - это не что иное, как среднее квадратов отклонений. С другой стороны, стандартное отклонение является среднеквадратичным отклонением.
- Дисперсия обозначается сигма-квадратом (σ2), тогда как стандартное отклонение обозначается как сигма (σ).
- Дисперсия выражается в квадратных единицах, которые обычно больше, чем значения в данном наборе данных. В отличие от стандартного отклонения, которое выражается в тех же единицах, что и значения в наборе данных.
- Дисперсия показывает, насколько далеко распределены люди в группе. И наоборот, стандартное отклонение измеряет, насколько наблюдения набора данных отличаются от его среднего значения.
иллюстрация
Оценки, выставленные студентом по пяти предметам, составляют 60, 75, 46, 58 и 80 соответственно. Вы должны узнать стандартное отклонение и дисперсию.
Прежде всего, вы должны узнать среднее значение,

Таким образом, средняя (средняя) оценка составляет 63, 8
Теперь вычислим дисперсию
| Икс | (XA) | (ХА) ^ 2 | |
|---|---|---|---|
| 60 | 63, 8 | -3, 8 | 14, 44 |
| 75 | 63, 8 | 11, 2 | 125, 44 |
| 46 | 63, 8 | -17, 8 | 316, 84 |
| 58 | 63, 8 | 5, 8 | 33, 64 |
| 80 | 63, 8 | 16, 2 | 262, 44 |
Где X = наблюдения
A = среднее арифметическое
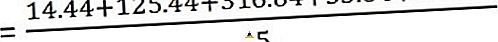
И стандартное отклонение -

сходства
- Дисперсия и стандартное отклонение всегда положительны.
- Если все наблюдения в наборе данных идентичны, то стандартное отклонение и дисперсия будут равны нулю.
Заключение
Эти два основных статистических термина, которые играют жизненно важную роль в различных секторах. Стандартное отклонение предпочтительнее среднего, поскольку оно выражается в тех же единицах, что и измерения, в то время как отклонение выражается в единицах, превышающих данный набор данных.









