Идеальная мера центральной тенденции - это та, которая четко определена, легко понятна, просто вычисляема. Он должен основываться на всех наблюдениях и быть наименее затронутым экстремальными наблюдениями, присутствующими в наборе данных.
Люди часто противопоставляют эти два показателя, но факт в том, что они разные. Эта статья особо подчеркивает основные различия между средним и средним. Посмотри.
Сравнительная таблица
| Основа для сравнения | Имею в виду | медиана |
|---|---|---|
| Имея в виду | Среднее значение относится к простому среднему значению данного набора значений или величин. | Медиана определяется как среднее число в упорядоченном списке значений. |
| Что это? | Это среднее арифметическое. | Это позиционное среднее. |
| Представляет собой | Центр тяжести набора данных | Центр тяжести набора данных Средняя точка набора данных |
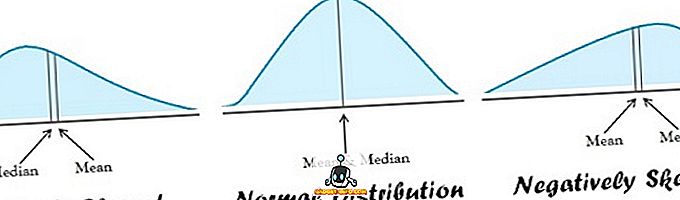
| применимость | Нормальное распределение | Перекошенное распределение |
| Выпадающие | Среднее чувствительно к выбросам. | Медиана не чувствительна к выбросам. |
| расчет | Среднее значение рассчитывается путем суммирования всех наблюдений и последующего деления полученного значения на количество наблюдений. | Чтобы вычислить медиану, набор данных располагается в порядке возрастания или убывания, тогда значение, которое попадает в точную середину нового набора данных, является медианой. |
Определение среднего
Среднее значение - это широко используемая мера центральной тенденции, которая определяется как среднее из набора значений. Он представляет модель и наиболее распространенное значение заданного диапазона значений. Его можно рассчитать как в дискретных, так и в непрерывных рядах.
Среднее значение равно сумме всех наблюдений, деленной на количество наблюдений в наборе данных. Если значение, принятое переменной, равно, ее среднее значение также будет таким же. Среднее значение может быть двух типов: среднее по выборке (x̅) и среднее по популяции (µ). Его можно рассчитать по заданной формуле:
- Среднее арифметическое :

n = количество значений - Для дискретных серий :

- Для непрерывного обслуживания :

A = предполагаемое среднее
C = общий делитель
Определение медианы
Медиана является еще одной важной мерой центральной тенденции, используемой для разделения значения на две равные части, то есть большую половину выборки, совокупности или распределения вероятностей из нижней половины. Это среднее значение, которое достигается, когда наблюдения сортируются в определенном порядке, в порядке возрастания или убывания.
Для вычисления медианы, в первую очередь, организуйте наблюдения в порядке убывания или от максимума до минимума, затем примените соответствующую формулу согласно условиям, приведенным ниже:
- Если число наблюдений нечетно :

- Если число наблюдений четное :

- Для непрерывных серий :

c = накопленная частота предыдущего среднего класса
f = частота среднего класса
h = ширина класса
Ключевые различия между средним и медианным
Существенные различия между средним и средним приведены в статье ниже:
- В статистике среднее определяется как простое среднее заданного набора значений или величин. Медиана называется средним числом в упорядоченном списке значений.
- В то время как среднее значение является средним арифметическим, медиана является средним позиционным значением, по сути, положение набора данных определяет значение медианного значения.
- Среднее обозначает центр тяжести набора данных, тогда как медиана выделяет самое среднее значение набора данных.
- Среднее значение подходит для нормально распределенных данных. С другой стороны, медиана является лучшей, когда распределение данных искажено.
- Среднее значение сильно зависит от экстремального значения, которого нет в случае с медианой.
- Среднее значение рассчитывается путем суммирования всех наблюдений, а затем деления полученного значения на количество наблюдений; результат подлый. В отличие от медианы, набор данных располагается в порядке возрастания или убывания, тогда значение, которое попадает в точную середину нового набора данных, является медианой.
пример
Найдите среднее значение и медиану данного набора данных:
58, 26, 65, 34, 78, 44, 96
Решение: чтобы вычислить среднее значение, вам нужно разделить сумму наблюдений на количество наблюдений,

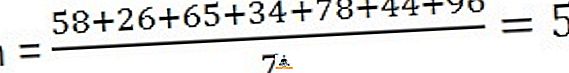
Для вычисления медианы, прежде всего, расположите ряды в последовательности, то есть от низшего к высшему,
26, 34, 44, 58, 65, 78, 96
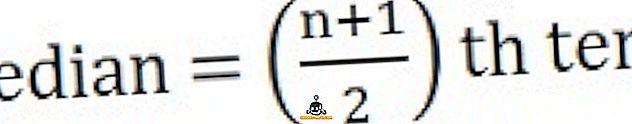
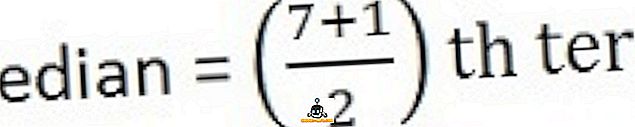
Заключение
Изучив вышеприведенные пункты, можно сказать, что эти два математических понятия различны. Среднее арифметическое или среднее значение считается лучшей мерой центральной тенденции, поскольку оно содержит все признаки идеальной меры, но имеет один недостаток, заключающийся в том, что колебания выборки влияют на среднее значение.
Таким же образом, медиана также однозначно определена и проста для понимания и расчета, и самое лучшее в этой мере - то, что на нее не влияют колебания выборки, но единственным недостатком медианы является то, что она не основана на всех наблюдения. Для классификации с открытым концом медиана обычно предпочтительнее средней.